Najpiękniejsza formuła
Cztery słynne liczby i najpiękniejsze równanie matematyki
Liczba π
π = 3,141592 653589 793238 462643 383279 502884 197169...
Pole koła o promieniu jeden jest równe π. Próby wyznaczenia tej liczby podejmowali już ok. 1800 r.p.n.e. Babilończycy szacowali jej wartość na 3 i 1/8, a Egipcjanie na ok. 3,1605 (28/34) w papirusie Rhinda datowanym na 1650 r.p.n.e.
Ludolf van Ceulen pod koniec XVIw. poświęcił dużą część swojego życia na coraz dokładniejsze wyznaczenie liczby π. Przed śmiercią zdołał poprawić jej dokładność do 35 miejsca po przecinku. Dlatego w Niemczech nazywa się ją liczbą Ludolfa, a w Polsce niekiedy Ludolfiną. Dzisiaj tego rodzaju obliczeniami zajmują się komputery.
W 430 r. n.e. astronom chiński Tsu Chung-chih podał wartość π w postaci ułamka 355/113, choć wiemy, że nie jest to liczba wymierna. Ok. roku 600 n.e. matematyk hinduski Brhmagupta podał wartość π jako √10 = 3,16227766... Jednak liczba π nie jest równa żadnemu ułamkowi i nie jest pierwiastkiem kwadratowym żadnego ułamka. Udowodnił to w roku 1761 niemiecki matematyk Lambert. W roku 1882 Lindemann udowodnił, że liczba π jest liczbą przestępną, tzn. iż nie jest pierwiastkiem żadnego wielomianu o współczynnikach całkowitych.
Liczba 0
Tradycyjny system liczenia nie obejmuje liczby zero, bowiem gdy nie ma co policzyć nie ma co używać liczb. Jednak taki sposób podejścia doprowadził do tego, że nie ma roku zerowego i nie ma też godziny zero, gdyż wtedy doba miałaby 23 godziny.
Ok. VIw. matematycy hinduscy połączyli trzy wielkie idee zapisu matematycznego liczb. Zasadę zapisu pozycyjnego, oddzielenie liczb od obiektów rzeczywistych i wprowadzenie zera jako wartości zerowej. Wielki matematyk i astronom hinduski Brahmagupta w swoim dziele z roku 628 przedstawia sposoby szybkiego wykonywania sześciu działań (dodawania, odejmowania, mnożenia, dzielenia, potęgowania i pierwiastkowania) na obiektach, które nazwał dobrem, długiem i nicością. Uczony ten odkrył, że dług odjęty od nicości staje się dobrem, a dobro odjęte od nicości staje się długiem.
Liczba 1
Podzielnik wszystkich liczb pierwszych sam za taką nie jest uważany. Matematycy dostrzegli odrębność jedynki lokując ją w odrębnej klasie jedności. Taką rolę odgrywa ona w algorytmie do wyznaczania liczb pierwszych znanym pod nazwą sito Eratostenesa (276 - 194 p.n.e.), kustosza Biblioteki Aleksandryjskiej.
Każde zwielokrotnienie coraz mniejszej liczby dodatniej przez nią samą zbliża do jedności:
lim xx = 1
x→0+
0,10,1 = 0,794
0,010,01 = 0,955
0,0010,001 = 0,993
0,00010,0001 = 0,999
...................
Liczba e
e = 2,718281 828459 045235 360287 471352 662497 757247...
Liczba Napiera (Nepera) e jest podstawą logarytmu naturalnego. W matematyce logarytmy naturalne definiuje się jako pola zawarte pod wykresem funkcji 1/x. Na rysunku przykład przedstawiający interpretację geometryczną logarytmu naturalnego z liczby a (ln a).

lim (1 + 1/n)n = e
n→∞
lub
lim (1 + x)1/x = e
x→0
Najpiękniejsze równanie matematyki
Definicja liczby ex jako granicy ciągu (1 + x/n)n jest prawidłowa także dla liczb zespolonych x. Tak więc eiπ jest określone granicą ciągu (1 + iπ/n)n, która dla dużych wartości n zbliża się do -1.

Rysunek pokazuje, że pomnożenie n-krotne liczby zespolonej 1 + iπ/n dokonuje się przez n-krotne skręcenie punktu reprezentującego tę liczbę, aż osiągnie on położenie -1. Jeśli tak, to otrzymujemy najpiękniejsze równanie matematyki:
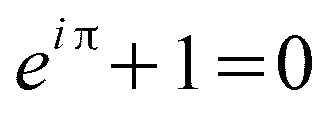
Pojawia się ono w dziele Eulera (1707 - 1783) Introductio opublikowanym w Lozannie w roku 1748. Równanie to zawiera i wiąże we wzajemnej relacji symbole liczb najbardziej ekscytujących ludzi interesujących się matematyką.
i = √-1 jest w tym przypadku raczej symbolem operatora niż liczby.